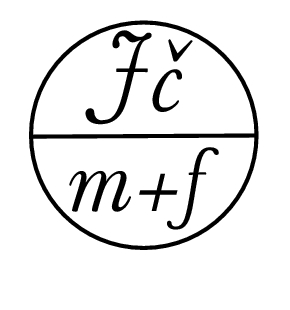Kdy: čtvrtek 20. ledna 2022, od 14:00 (délka: 1 hodina včetně diskuse)
Kde: CP 1.03, přednášku je možno sledovat i online zde
Anotace
Mathematical model for macromolecule catalytic conversion in a flow reactor includes four interconnected numerical calculations of different scales for the following phenomena: effect of increasing the concentration of coke grains and their size (nanometers, scale of coke particles) on porosity, tortuosity, and specific area of the catalyst computing percolation graphs of the mesoporous and hierarchically porous catalysts (dozens of nanometers, scale of percolation graph); kinetic patterns for asphaltene conversion and catalyst deactivation in the mesoporous and hierarchically porous pellets (millimeters, catalyst pellet scale); macrokinetic model for reactor operation filled with mesoporous and hierarchically porous pellets (centimeters, reactor scale). Mathematical instruments involves both discrete (Lubachevsky-Stillinger, Dijkstra algorithm) and continuous (Fick’s law, kinetic equations) methods. Striking difference in the texture evolution of mesoporous and hierarchical catalysts was observed by both catalytic experiments and theory, during asphaltene conversion (HDAs) resulted in fast deactivation of the first catalyst while the second one showed a long-term stability.
O přednášejícím
doc. Ya. V. Bazaikin, Ph.D., D.Sci.
Sobolev Institute of Mathematics, Novosibirsk, Russia, head of Laboratory of Riemannian Geometry and Topology
Hlavní směry výzkumu:
- The development of multi-scale mathematical models of physical and chemical processes in porous media with complex hierarchical structure and the development of numerical methods for calculating these models, especially processes accompanied by a significant change in the pore space. This category, for example, includes sintering of sorbents in the process of sorption, dissolution of the rock matrix during the injection of a reactive fluid, deactivation of catalysts in the process of hydrocracking of heavy hydrocarbons, modeling of mercury and nitrogen porosimetry of a porous body, etc. In particular, the creation of algorithms for calculating the geometric and topological characteristics of the medium on a pore scale and their computer implementation.
- Differential geometry, in particular, theory of holonomy groups of Riemannian and Lorentzian manifolds, the theory of Einstein manifolds, the theory of foliations, integrable geodesic flows, positive curvature, and global shape.